|
|
|
 |
THE PYTHAGOREAN THEOREM is possibly 4000 years old! |  |
| THE PYTHAGOREAN THEOREM 2000 B.C. The Pythagorean Theorem is quite well-known, but no one knows very much about the man, for whom the famous theorem is named or how the result was first proved. The real "Pythagoras" was an African, whose name has long been forgotten. How else could the ancient Egyptians have built pyramids without using the most famous equation about triangles, the Pythagorean Theorem? The Pythagorean Theorem states that, for a right triangle with sides of lengths, a and b, respectively, and hypotenuse of length c, (a)(a) + (b)(b) = (c)(c) |
 |
|
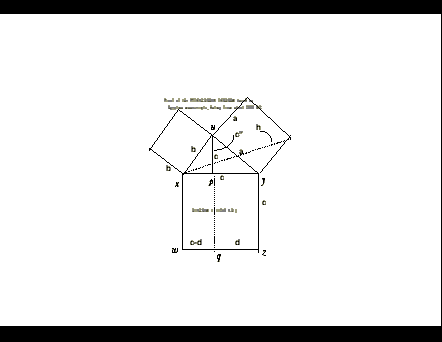
| A MYSTERIOUS DIAGRAM There is a mysterious diagram, torn from an Arabian manuscript, and thought to date from 1258 A.D., which is said to be a proof of the Pythagorean Equation. There is a photo of this diagram in the book, AFRICA COUNTS by Claudia Zaslavsky. I had seen the diagram in many high school textbooks, but the explanation of it was always missing. It was adorned and modified in various ways, according to each illustrator's fancy. To all appearances, it might have been worn as a hat, as far as what was stated about its true meaning. Considering the mystery of its origins, I suspect the diagram might even date back from before 1258 A.D. More ancient diagrams are decoded at Ancient African Astronomy |
ARABIAN PROOF 1258 A.D.The above diagram (without lettering) was torn from an old Arabian manuscript.That this is a proof of the Pythagorean Theorem is demonstrated by using the axiom of the inclination of the pyramid given in the RHIND PAPYRUS 2000 B.C. |
|
THE AXIOM OF THE INCLINATION OF THE PYRAMID
|
EXAMPLE FROM THE RHIND PAPYRUS.The inclination, as defined in the Rhind Papyrus, is measure in units of "hand breadths." (It is believed a "hand breadth" was about 4 inches.) Technically, the inclination is defined to be "the number of units by which the inclined plane departs from the vertical for a rise of one cubit." (A cubit is about 7 "hands.")QUESTION:Suppose 360 is the base of a triangle and 250 is its height. What is the inclination? ANSWER: (250)(I(u)) = inclination = u(180) cubits. From the above example, it is clear that the inclination, I(u), is the base of the right triangle determined by the vertical line segment "u." And it is calculated by comparing the ratio of sides of similar right triangles. |
|